
L’Onde est un streptoèdre,
Du grec ancien στρεπτός, streptos («tourné») et ἕδρα, hedra («siège, base», et par extension «face d’un solide géométrique»).
Le streptoèdre a 2 faces, 1 seule arête, 0 sommet, et est issu d’un solide à 3 faces, 2 arêtes et 0 sommet.
Mais comment est-ce possible?
Reprenons depuis le début :
Au commencement était le polygone : c’est un une figure à plusieurs côtés (ex : pentagone : 5 côtés, hexagone : 6 côtés).
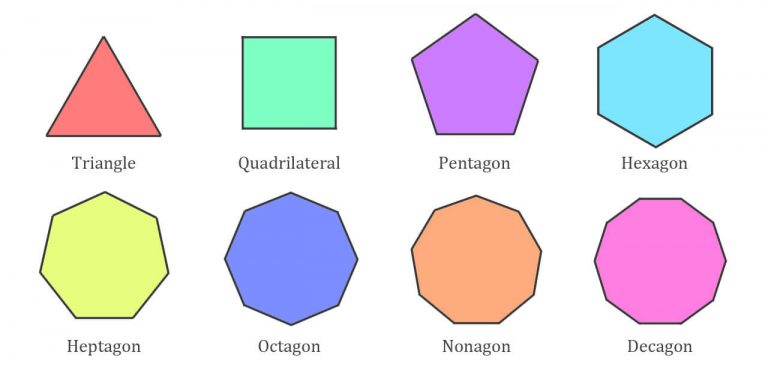
Puis vint le polyèdre : c’est un volume à plusieurs faces (ex : pentaèdre : 5 faces, hexaèdre : 6 faces)
Le mot polyèdre, provient des racines grecques πολύς (polys), «beaucoup» et ἕδρα (hedra), «base», «siège» ou «face».
Un polyèdre est un solide dont toutes les faces sont des polygones. Les côtés de ces polygones sont appelés arêtes. Les extrémités des arêtes sont des points appelés sommets.
Par exemple, une pyramide (qui est un tetraèdre) possède 4 faces, 6 arêtes et 4 sommets.
A côté des polyèdres, nous trouvons d’autres solides qui possèdent également des faces, des arêtes et des sommets, ce sont les cônes (2 faces, 1 arête, 1 sommet), cylindres (3 faces, 2 arêtes) et sphères (1 face).
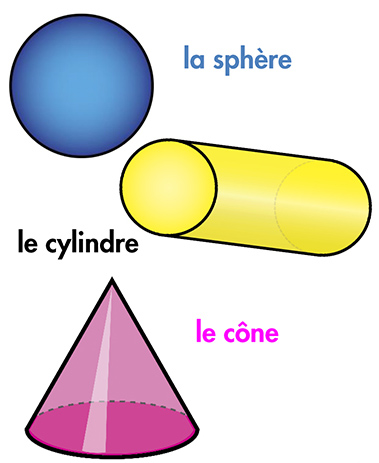
Prenons un cylindre (donc 3 faces et 2 arêtes) et coupons le en 2 dans le sens de la longueur; en l’ouvrant, nous obtenons la figure d’un polygone de chaque côté, soit rectangle si la longueur du cylindre est supérieure au diamètre, soit carré, si la longueur est égale au diamètre.
Rajoutons à ce dernier cas de figure, des courbes symétriques (de même rayon) en bois de fil et en bois de bout (puisque l’on parle de tournage sur bois), et voici ce que l’on obtient.
Des 2 pièces tournées de 90° naît le streptoèdre, qui n’a plus que 2 faces et 1 seule arête! Magique!!!
C’est ainsi que naquit l’Onde…






